Ideas for MRISC32 vector operations

This time I want to talk about some future directions for the MRISC32 vector model. For a recap, see: The MRISC32 – A vector first CPU design.

The vector model that was chosen for the MRISC32 instruction set architecture has already proven itself successful. Since it has been implemented in the single-issue, in-order CPU MRISC32-A1, it has become clear that:

• It is very easy to implement in hardware, even in power-efficient in-order architectures, and it can be designed to use a minimum of additional resources since the scalar execution units can be used for both scalar and vector operations.
• Vector operations can give significant performance gains for an in-order CPU, especially in areas like memory access and floating-point computation where latencies are high (since virtually all data dependency hazards go away).
• As a software developer, it is easy to use the functionality. Often it is mostly just a matter of replacing scalar registers with vector registers in the assembly code (since most instructions work exactly the same way in scalar and vector mode).

Furthermore it is anticipated that the same vector model will be successful in highly parallel architectures too, since:

• Vector execution can be fully parallel (execution unit width = vector register with), fully serial (execution unit width = 32 bits, vector register width = 2^N * 32 bits), or somewhere in between – the software model is the same.
• There is no limit to how wide vector registers and execution units the ISA can support – even with binary software compatibility with narrower, low end architectures.

However, some functionality is not really finalized yet (mostly because I have not been sure how to implement it in hardware), which currently limits the efficiency and usefulness of vector operations.

Edit: Some parts of the ISA have changed since this article was written. See the latest MRISC32 Instruction Set Manual.

The good

I recently implemented a vectorized version of the calculation the Mandelbrot set. Since the algorithm is floating-point heavy with lots of data dependencies (every value in an iteration depends on the previous value), the scalar version resulted in lots of pipeline stalls.

In the vector version, four adjacent pixels are processed in parallel. Here is an excerpt of the core loop:

  fmul    v5, v3, v3  ; v5 = z.re^2
  fmul    v6, v4, v4  ; v6 = z.im^2
  fadd    v7, v5, v6  ; v7 = |z|^2
  fslt    v8, v7, r9  ; |z|^2 < 4 (r9)?

As you can see, two of the four instructions have dependencies on the previous instruction. If these were scalar operations (acting on R-registers instead of V-registers), those instructions would stall for three cycles each (since fmul & fadd have a latency of three cycles).

In the vector version all stalls are eliminated, since by the time a vector instruction starts and needs the first input vector element, the previous vector instruction has finished the work on the first vector element (it has just started the work on the last vector element). Thus the pipeline is filled at all times without any bubbles.

So far so good. However, the Mandelbrot algorithm has an iteration termination criterion: if |z|² ≥ 4 we should stop the iteration. The corresponding comparison is the last instruction in the example above.

The bad

We need to terminate (branch) once all vector elements satisfy the condition. How do we do that? Unfortunately, we currently have to do this:

  ldi     vl, #2        ; Fold-length = 2
  or/f    v9, v8, v8    ; Folding OR
  ldi     vl, #1        ; Fold-length = 1
  or/f    v9, v9, v9    ; Folding OR

  stw     v9, r10, #0   ; Store 1 vector element on the stack
  ldw     r11, r10, #0  ; Load value into a scalar register
  ldi     vl, #4        ; Restore vector length = 4
  bz      r11, done     ; Done if all elements are false

In the code above the four first instructions fold the four vector element results into a single element, in two steps like this:

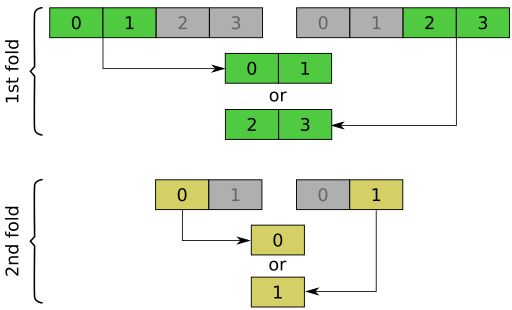
Now V9[0] == FALSE only if all elements of V8 were FALSE.

The next four instructions transfer the vector element V9[0] to a scalar register (R11), via the stack, and uses that scalar register to perform the conditional branch (this is because branch instructions can only act on scalar registers).

Improvements

Here are some additions tho the ISA that would improve the situation significantly (these are all planned, but not yet implemented)…

Transfer vector element to scalar register

An obvious deficiency is that we have to transfer data from a vector register to a scalar register via memory (store + load). A simple addition to the MRISC32 instruction set is an instruction that moves a single vector element to a scalar register. Then we would get:

   ldi     vl, #2        ; Fold-length = 2
   or/f    v9, v8, v8    ; Folding OR
   ldi     vl, #1        ; Fold-length = 1
   or/f    v9, v9, v9    ; Folding OR
   ldi     vl, #4        ; Restore vector length = 4
   vmov    r11, v9, #0   ; Move v9[0] to r11
   bz      r11, done     ; Done if all elements are false

This extra instruction is fairly uncontroversial, and would only require minimal changes to the MRISC32-A1 implementation.

Add a length state to vector registers

If we add a vector length state to each vector register, we do not have to set the VL register explicitly when doing the folding operations.

The vector length state would be updated each time a vector register is written, and the length of a vector operation would be the length state of the first source operand. In the case of folding, the operation length would be half of the length of the first source operand. The VL register would only be used for the few operations that initialize a vector register (e.g. memory loads and operations involving the VZ register).

Now the code would be simplified to:

   or/f    v9, v8, v8    ; Folding OR
   or/f    v9, v9, v9    ; Folding OR
   vmov    r11, v9, #0   ; Move v9[0] to r11
   bz      r11, done     ; Done if all elements are false

This change is more complex. The trick is that you essentially need to read the vector length property before register fetch, but it is certainly doable.

Add a “bit set” state to vector registers

We could add an extra state to each vector register that has three possible values :

• -1 – All bits of all vector elements are set (1).
• 0 – All bits of all vector elements are cleared (0).
• +1 – At least one bit of any vector element is set (1) and at least one bit of any vector element is cleared (0).

We could add an instruction to query the bit set state of a vector register and transfer it to a scalar register. If we extend the planned “VMOV” instruction so that element index -1 represents the bit set state, we get the following code:

   vmov    r11, v8, #-1  ; Get bit set state of v8
   bz      r11, done     ; Done if all elements are false

Adding the bit set state to every vector register is non-trivial (but still doable). We essentially need to add an extra stage after a result is produced (by any pipeline, ALU, FPU, memory, …) that keeps track of all vector element values that are being produced. This may add complexity to operand forwarding etc, and probably requires one cycle of latency (the state will be updated after all the vector elements have been produced).

Enable vector registers as branch conditions

With the bit set state of the vector registers in place, we can make it possible to use a vector register as the branch condition. I.e. using a vector register as the branch condition will simply read the bit set state from the corresponding register and act on that. If so, we would get the following useful branch instructions:

Instruction	Meaning
bz v1, foo	Branch if all elements of v1 are false
bs v1, foo	Branch if all elements of v1 are true
bnz v1, foo	Branch if at least one element of v1 is true
bns v1, foo	Branch if at least one element of v1 is false

With this functionality, we would be able to reduce the eight instructions to the following compact code:

  bz      v8, done     ; Done if all elements are false

This functionality would be fairly simple to add to the hardware and to the instruction set. We would essentially only need to sacrifice one bit of conditional branch distance (we currently have 21 bits for the distance, which is much more than you typically need for a conditional branch). We would also have to add some extra decoding logic, but that should be negligible.

One more thing: Masked stores

Another thing that prevents some algorithms from being fully vectorized with the current MRISC32 ISA is its lack of masked memory store operations.

Many operations can already be performed conditionally quite naturally, e.g. using the SEL instruction that was presented in MRISC32 conditional moves, or using other logic/select operations (e.g. AND, or MIN/MAX, etc). However, conditionally storing a few selected vector elements to memory is not easily done without dedicated instructions.

An example is view frustum culling in computer graphics: Do not draw primitives or pixels that are outside of view. For instance, you may use 2D or 3D coordinates to calculate the on-screen location of a pixel, and furthermore calculate the corresponding memory address of that pixel. If a vector element represents an off-screen pixel, that memory store operation must not be performed.

One solution could be to hardwire one of the vector registers (e.g. V31) to masked operations, and call it VM (for “vector mask”). Further we can add one or more special instructions that implicitly use the VM register as a mask.

For instance, a masked “store word” instruction for scatter operation could have the following signature:

    stwm    v1, r1, v2  ; v1[i] => MEM[r1 + v2[i]], if vm[i] is true

Some open questions are:

• What store operations should have masked versions (word, half-word, byte, gather/scatter, stride-based)?
• Should the VM register be treated as a purely boolean mask, or as a byte select mask? The latter would allow for masking of packed data types too (e.g. in combination with a SEQ.B instruction).
• Should other types of instructions also have masked variants? E.g. masked loads can be useful, especially in a machine with an MMU (not yet implemented in MRISC32) with possible page faults for invalid addresses.

Implementation-wise, the relevant bits of the VM register could be kept in a dedicated mirror register, so that we do not need to waste a generic vector register read port for masked operations.

That’s it for this time!